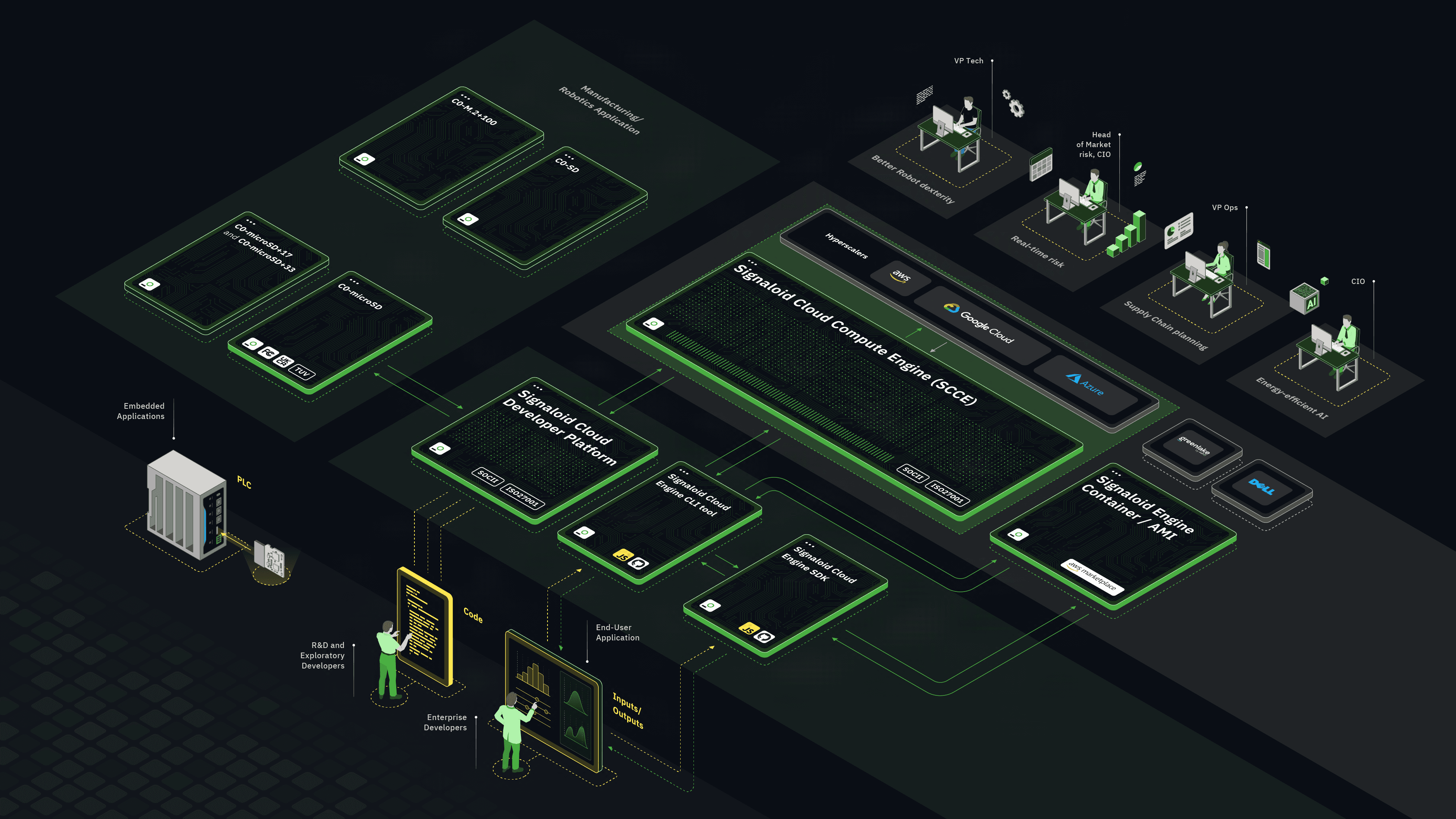
Technology Explainers
Compatibility with your existing CPU and GPU infrastructure, efficient digital representations of probability distributions, and efficient arithmetic on probability distributions. The technology explainers below provide more details on how Signaloid's technology works, from the underlying mathematics to the engineering implementation and applications.