Technology Explainer

#

02

Use Geometry to Estimate π

Estimate π With Geometry and Deterministic Arithmetic On Probability Distributions

There are many mathematical problems that can be reformulated in terms of geometry. For example, the numerical value of π is defined by geometry as the ratio of the circumference of a circle to its diameter, or as four times the ratio of the area of a quadrant of a disk to the square of its radius. The second of these geometric interpretations also provides an easy-to-visualize geometric approach to estimating the value of π.

Why It Matters

This example highlights a method for estimating the value of π using a combination of geometry and the capabilities of the Signaloid compute platform's ability to perform deterministic arithmetic on probability distributions. It provides a starting point for creating more advanced algorithms.

The Technical Details

A traditional Monte Carlo implementation of the geometric estimation of π would first generate coordinates within the disk of radius r, that is, pairs (x, y) where x and y are each chosen to be uniformly distributed between 0 and the radius r. For each generated pair, a Monte Carlo implementation would check if the point satisfies the condition that the square of the x- and y-coordinate values should be less than the square of the radius. The Monte Carlo implementation would count the fraction of generated points that satisfy this check and would divide the count by four to get an estimate of π. The main insight in creating a version of this algorithm for execution on the Signaloid compute platform is that, rather than generating samples and checking them individually, the algorithm can be formulated directly in terms of probability distributions, treating probability distributions as a first-class value type in algorithms.

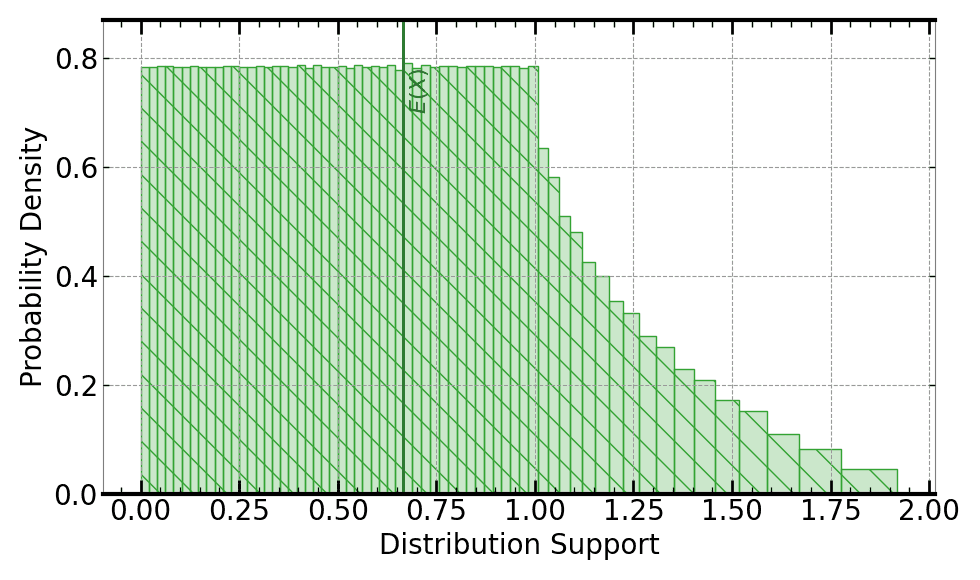
Plot of distribution of the square of the Euclidean distance between an uncertain location with uniformly-distributed x- and y- coordinate values, and the origin, computed as the sum of the squares of the uniformly-distributed x- and y- coordinates.
Plot of distribution of the square of the Euclidean distance between an uncertain location with uniformly-distributed x- and y- coordinate values, and the origin, computed as the sum of the squares of the uniformly-distributed x- and y- coordinates.

Distribution of the square of the Euclidean distance between an uncertain location with uniformly-distributed x- and y- coordinate values, and the origin, computed as the sum of the squares of the uniformly-distributed x- and y- coordinates.

When running on the Signaloid compute platform, an algorithm can define the x- and y-coordinates as uniform distributions between 0 at the origin and radius, r, at the edge of the disk. The algorithm running on the Signaloid compute platform can then take the sum of the square of these distributions to obtain the square of the Euclidean distance between an uncertain location with uniformly-distributed x- and y- coordinate values and the origin; the plot above shows the distribution of this quantity. Finally, the algorithm can query the probability that the computed Euclidean distance is less than the square of the radius r; the estimate of π is four times this probability. The code example shows a complete program that you can run on the Signaloid Cloud Developer Platform.

Relevant Code Example

#include <stdio.h>
#include <math.h>
#include <uxhw.h>

int
main(int argc, char *  argv[])
{
	const double	quarterCircleRadius = 1.0;
	double			x, y, rSquared, probabilityPointIsInQuadrant;

	x = UxHwDoubleUniformDist(0, quarterCircleRadius);
	y = UxHwDoubleUniformDist(0, quarterCircleRadius);
	rSquared = pow(x, 2) + pow(y, 2);
	probabilityPointIsInQuadrant =  1 -
					UxHwDoubleProbabilityGT(rSquared,
					quarterCircleRadius);

	printf(
		"Square of distance, r^2, from coordinate (0, 0) can be computed "
		"directly as distribution of expression x*x + y*y "
		"and is equal to %lf.\n",
		rSquared);

	printf(
		"Probability that point with uniformly-distributed "
		"x- and y-coordinates is in quarter disk, i.e., "
		"Prob(r^2 < 1), is %lf.\n",
		probabilityPointIsInQuadrant);

	printf(
		"Estimated value of π is = %lf.\n",
		4*probabilityPointIsInQuadrant);

	return 0;
}
#include <stdio.h>
#include <math.h>
#include <uxhw.h>

int
main(int argc, char *  argv[])
{
	const double	quarterCircleRadius = 1.0;
	double			x, y, rSquared, probabilityPointIsInQuadrant;

	x = UxHwDoubleUniformDist(0, quarterCircleRadius);
	y = UxHwDoubleUniformDist(0, quarterCircleRadius);
	rSquared = pow(x, 2) + pow(y, 2);
	probabilityPointIsInQuadrant =  1 -
					UxHwDoubleProbabilityGT(rSquared,
					quarterCircleRadius);

	printf(
		"Square of distance, r^2, from coordinate (0, 0) can be computed "
		"directly as distribution of expression x*x + y*y "
		"and is equal to %lf.\n",
		rSquared);

	printf(
		"Probability that point with uniformly-distributed "
		"x- and y-coordinates is in quarter disk, i.e., "
		"Prob(r^2 < 1), is %lf.\n",
		probabilityPointIsInQuadrant);

	printf(
		"Estimated value of π is = %lf.\n",
		4*probabilityPointIsInQuadrant);

	return 0;
}
#include <stdio.h>
#include <math.h>
#include <uxhw.h>

int
main(int argc, char *  argv[])
{
	const double	quarterCircleRadius = 1.0;
	double			x, y, rSquared, probabilityPointIsInQuadrant;

	x = UxHwDoubleUniformDist(0, quarterCircleRadius);
	y = UxHwDoubleUniformDist(0, quarterCircleRadius);
	rSquared = pow(x, 2) + pow(y, 2);
	probabilityPointIsInQuadrant =  1 -
					UxHwDoubleProbabilityGT(rSquared,
					quarterCircleRadius);

	printf(
		"Square of distance, r^2, from coordinate (0, 0) can be computed "
		"directly as distribution of expression x*x + y*y "
		"and is equal to %lf.\n",
		rSquared);

	printf(
		"Probability that point with uniformly-distributed "
		"x- and y-coordinates is in quarter disk, i.e., "
		"Prob(r^2 < 1), is %lf.\n",
		probabilityPointIsInQuadrant);

	printf(
		"Estimated value of π is = %lf.\n",
		4*probabilityPointIsInQuadrant);

	return 0;
}

The Takeaway

The are many mathematical problems that can be reformulated in terms of geometry. This example highlights a method for estimating the value of π using a combination of geometry and the capabilities of the Signaloid compute platform's deterministic arithmetic on probability distributions.

Find Out More