Technology Explainer
#
01
Avoid Monte Carlo's Variability
Avoid Monte Carlo's Inherent Variability By Deterministic Computation on Probability Distributions
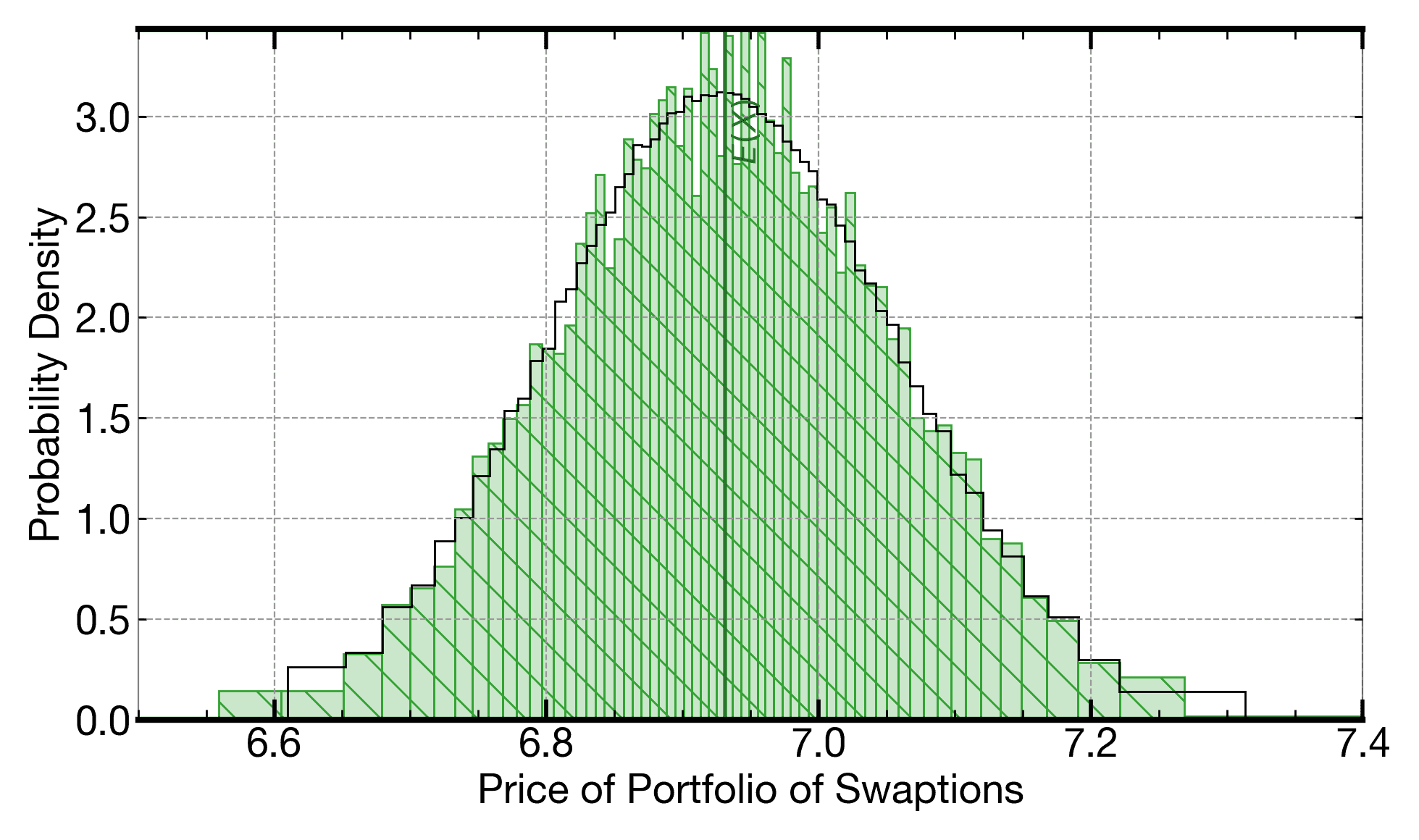
Monte Carlo execution repeatedly runs a computational kernel with parameter values drawn from some probability distribution. There are many variants of Monte Carlo, designed to speed up the sampling process, to make the sampling more homogeneous, etc., but they all share a common behavior: Each set of repetitions results in a measurably different distribution of final output. The plot below shows the output from one 8.9k-iteration Monte Carlo for a computational kernel that uses the Heath-Jarrow-Morton (HJM) framework to price a basket of swaptions. Each 8.9k-iteration Monte Carlo of this HJM kernel results in a slighly different distribution of the computed price of the basket of swaptions.
This plot shows the distribution generated from one 8.9k-iteration Monte Carlo of a kernel computing the price of a basket of swaptions by the Heath-Jarrow-Morton (HJM) framework (hatched region). The plot overlays the distribution from running a 1M-iteration Monte Carlo of the same kernel (outer outline line).
Why It Matters
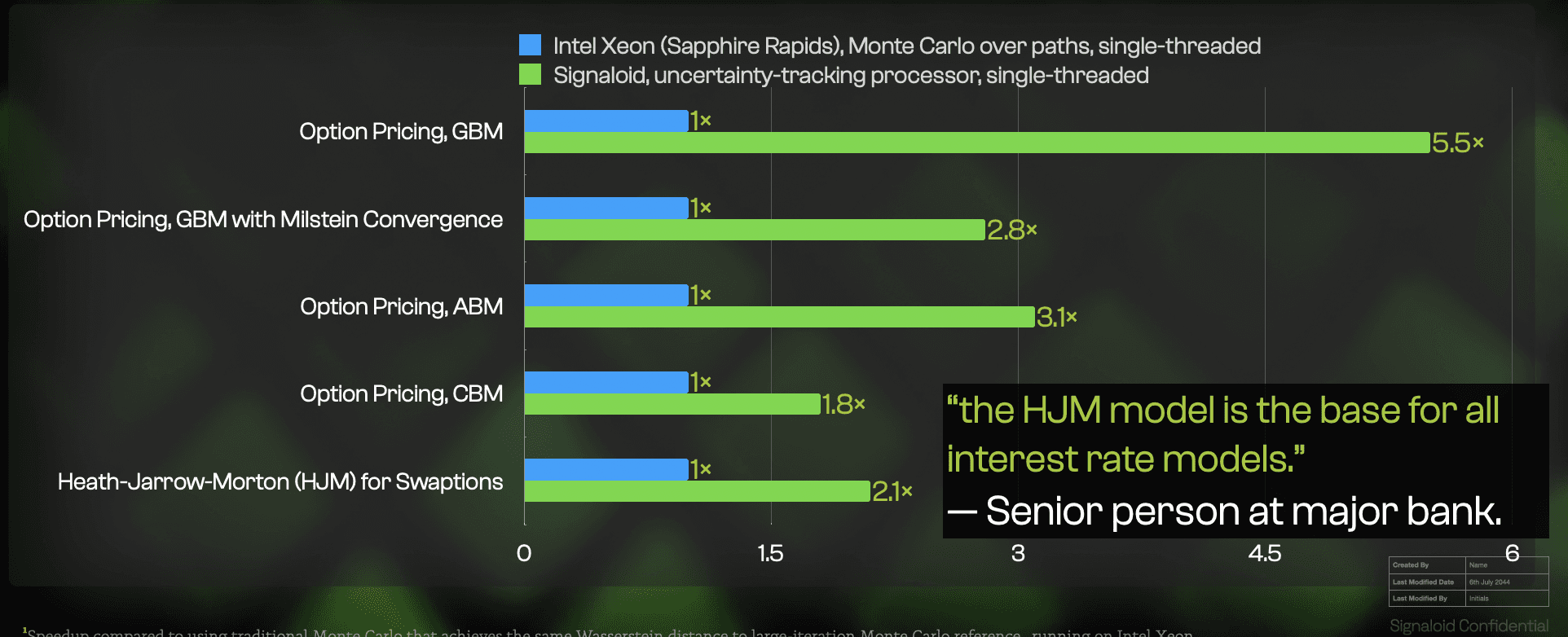
Computational kernels running on Signaloid's compute platform compute the same kinds of distribution outputs as a set of Monte Carlo repetitions, but with distributions that do not vary across executions. As a result, running your computational kernels on Signaloid's compute platform often provides stronger guarantees of convergence at the same time as providing faster execution (at least 2x faster and up to 120x faster, for an open benchmark based on the HJM framework and developed by Intel, as detailed below).
The Technical Details
For a given Signaloid core type such as C0Pro-XS or C0Pro-XL, the output obtained from running an application on Signaloid's platform is deterministic: It results in the same distribution each time. When benchmarking Signaloid's compute platform against Monte Carlo, we always report performance for a Signaloid core type for which the output distribution generated is consistently closer to the distribution generated by a large (e.g., 1M-iteration) Monte Carlo.
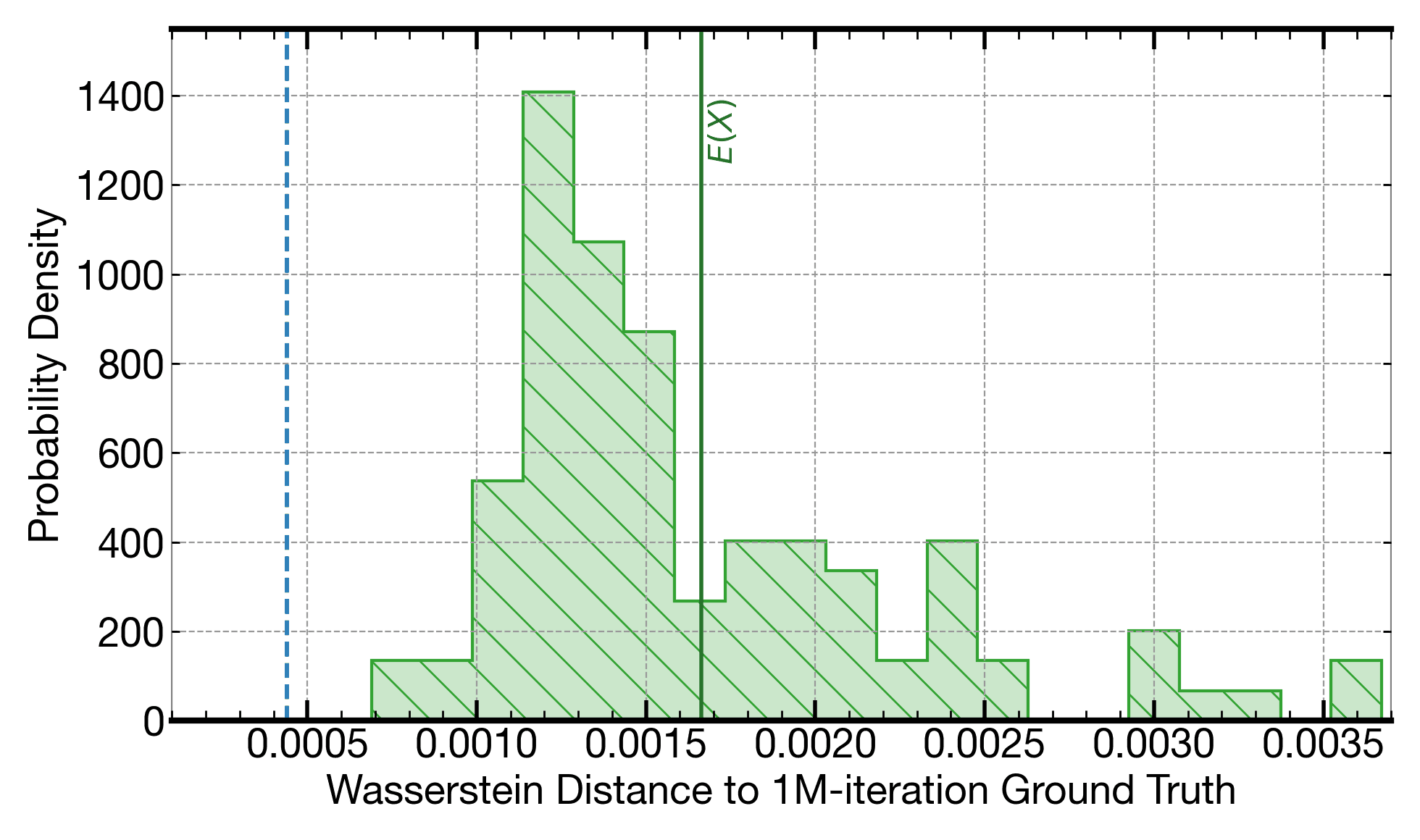
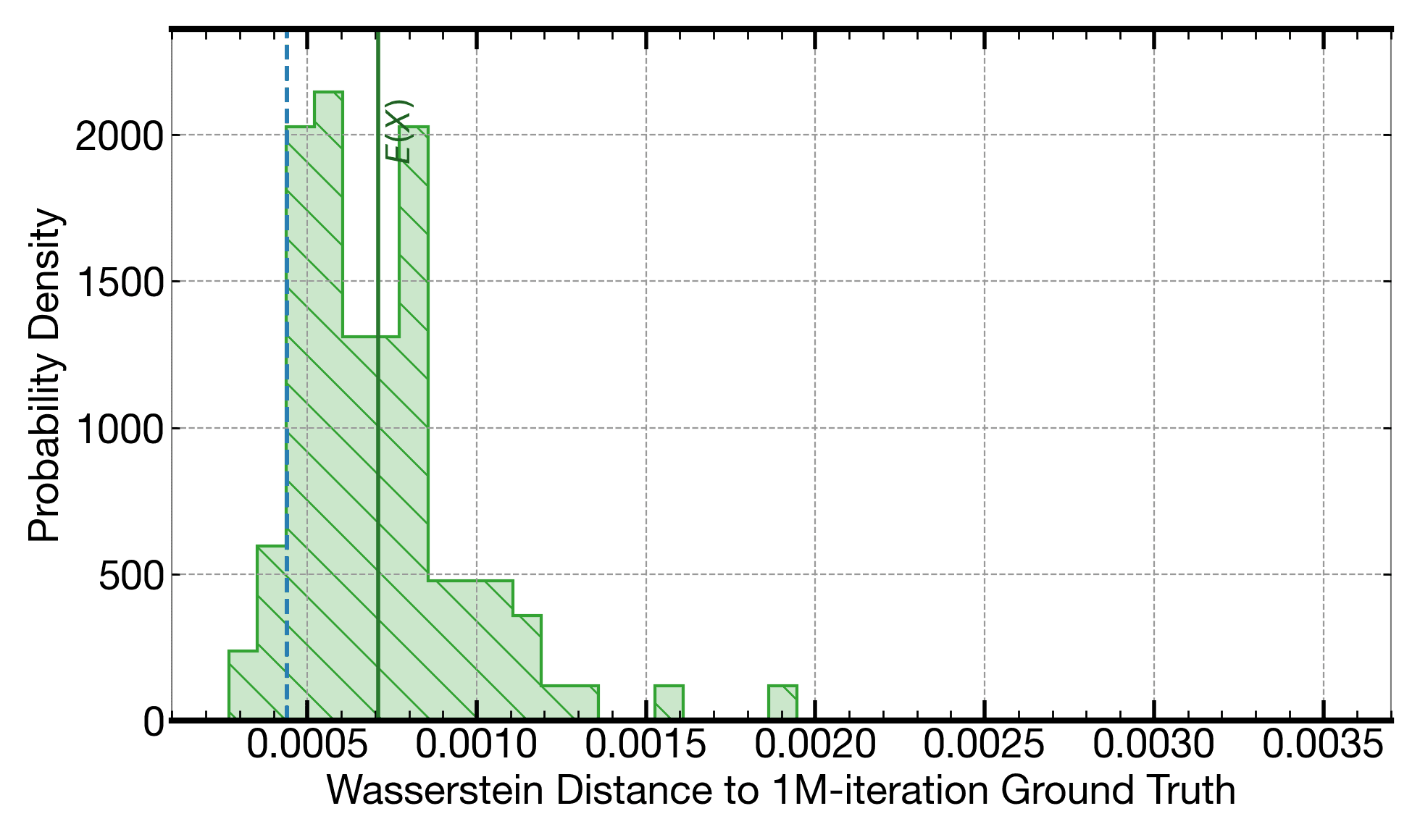
Any set of Monte Carlo executions will result in a slighly different output. This histogram shows the variation in Wasserstein distances to the output from a 1M-iteration Monte Carlo (as a quality reference) across several 8.9k-iteration Monte Carlo executions. The dashed vertical line shows the Wasserstein distance of the output generated when running on a C0Pro-XS core, which is fixed (and is consistently closest to the 1M-iteration Monte Carlo reference).
For an open benchmark based on the HJM framework and developed by Intel, for pricing a basket of swaptions using the Heath-Jarrow-Morton (HJM) framework, execution on Signaloid's C0Pro-XS core provides an output distribution that is consistently closer to the distribution of a 1M-iteration Monte Carlo, than 8.9k-iteration Monte Carlo: The vertical dashed line in the plot above is to the left of the hatched histogram. The solution running on Signaloid's platform is also consistently 2.7x faster, even before applying any parallelization (i.e., we compare a single-threaded implementation on Signaloid's platform to a single-threaded implementation on the comparison high-end Intel Xeon platform). The quality of the output when running on Signaloid's platform is even closer to the distribution of a 1M-iteration Monte Carlo, than some instances of 390k-iteration Monte Carlo executions, as the accuracy plots below show.
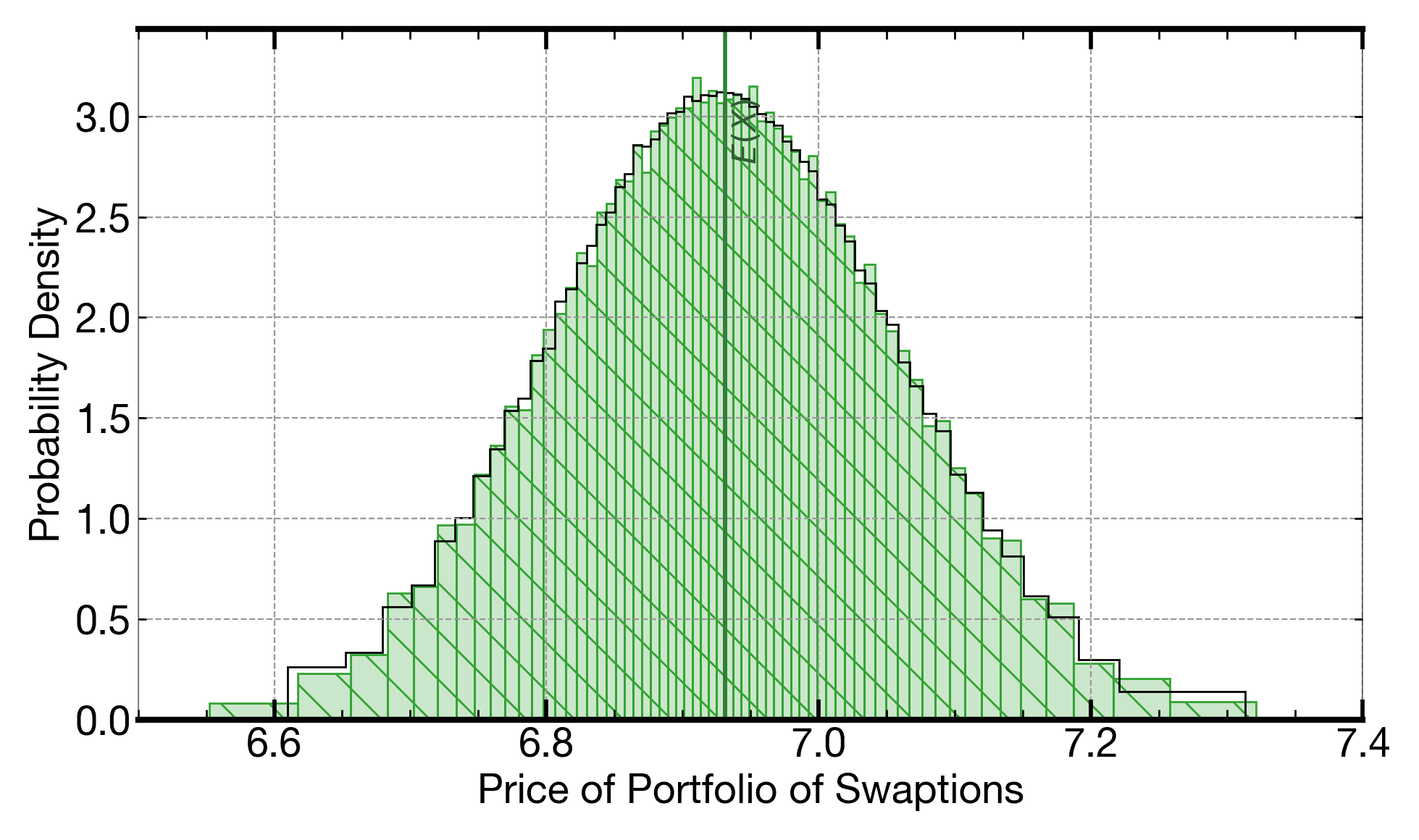
For the HJM kernel, the mean price of the basket of swaptions computed when running on a Signaloid C0Pro-XS core is within 0.1401 basis points of the mean price computed using a 1M-iteration Monte Carlo (one basis point is 0.01%). In comparison, the difference between the mean price of the basket of swaptions computed by 8.9k-iteration Monte Carlo and that computed using a 1M-iteration Monte Carlo, is between 0.3871 and 5.1649 basis points, varying across different batches of 8.9k-iteration Monte Carlo executions. Similarly, the difference between the mean price of the basket of swaptions computed by 390k-iteration Monte Carlo and that computed using a 1M-iteration Monte Carlo is between 0.0303 and 1.0755 basis points, varying across different batches of 390k-iteration Monte Carlo executions. The plots below show this variability in more detail.
Price of a basket of swaptions calculated using the HJM framework. The hatched distribution is the output distribution computed when running on a Signaloid C0Pro-XS core without using explicit Monte Carlo. This distributon is always the same and the computation is 2.7x faster than the 8.9k-iteration Monte Carlo, even before applying any parallelization (i.e., we compare a single-threaded implementation on Signaloid's platform to a single-threaded implementation on the comparison high-end Intel Xeon platform). The outline line on the plot shows the distribution from running a 1M-iteration Monte Carlo, used as a quality reference.
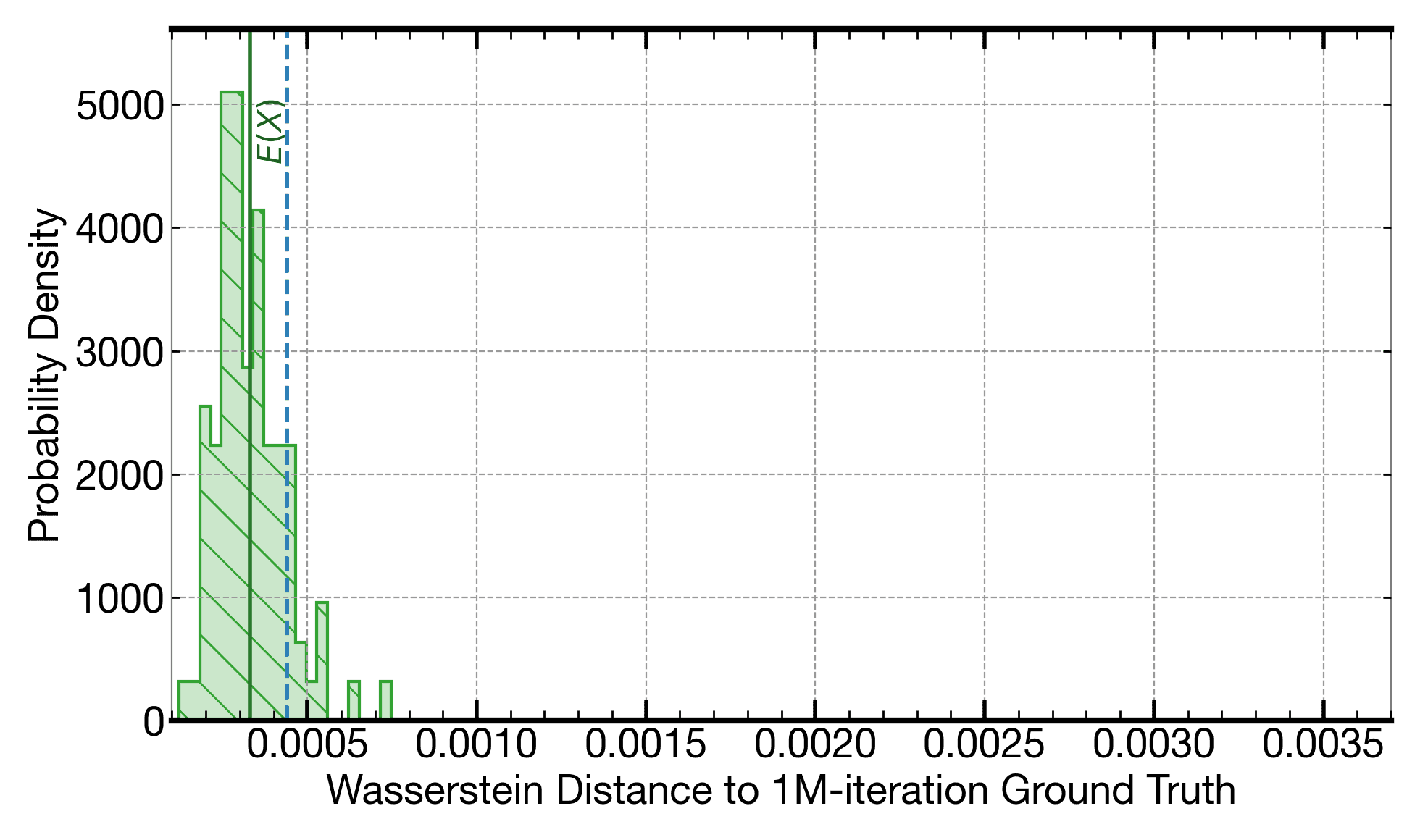
Histogram of Wasserstein distances to a 1M-iteration reference, of the distributions from re-runs of 65k-iteration Monte Carlo executions. The dashed vertical line shows the Wasserstein distance of the output generated when running on a C0Pro-XS core. The output of the kernel running on the C0Pro-XS is closer to the reference 1M-iteration Monte Carlo than most of the instances of the 65k-iteration Monte Carlo (and is more than 15x faster than them, even before applying any parallelization, i.e., we compare a single-threaded implementation on Signaloid's platform to a single-threaded implementation on the comparison high-end Intel Xeon platform).
Histogram of Wasserstein distances to a 1M-iteration reference, of the distributions from runs of 390k-iteration Monte Carlo executions. The dashed vertical line shows the Wasserstein distance of the output generated when running on a C0Pro-XS core. The latter is closer to the reference 1M-iteration Monte Carlo than several of the instances of the 309k-iteration Monte Carlo executions (and is more than 120x faster than them, even before applying any parallelization, i.e., we compare a single-threaded implementation on Signaloid's platform to a single-threaded implementation on the comparison high-end Intel Xeon platform).
The Takeaway
Each set of repetitions in a Monte Carlo execution results in a slightly different distribution of the Monte Carlo output. Signaloid's compute platform provides the same kinds of distribution outputs as a set of Monte Carlo repetitions, often providing distributions that are closer to a large 1M-iteration Monte Carlo but at a fraction of the computing time compared to even an 8k-iteration Monte Carlo. In contrast to sets of Monte Carlo executions, the distribution output from running on Signaloid's compute platform is deterministic and does not vary across executions. Because of this, using Signaloid's compute platform often provides stronger guarantees of convergence in addition to greater speed.